Experimento con botella PET: calentamiento de agua, pérdidas y curva tiempo–°C

Este es el Artículo 5 de la serie Proyectos de Energía Solar para Estudiantes. Llega después de: ¿Qué es la energía solar y cómo funciona?, la comparativa Térmica vs. Fotovoltaic, el proyecto Horno solar con cartón y papel aluminio y la Lámpara solar con botellas recicladas. Hoy mediremos de verdad cómo sube la temperatura del agua expuesta al Sol con ayuda de una botella PET y, sobre todo, por qué sube como sube.

1) La historia que vas a contar con datos

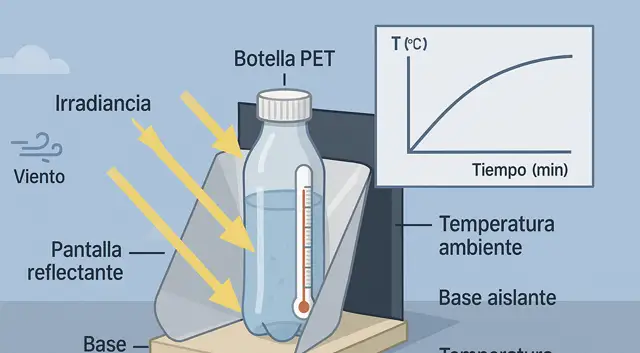
Imagina el patio de tu escuela a las 11:30. El piso brilla, los árboles apenas dan sombra y tú sostienes una botella PET con agua a temperatura ambiente. La dejas al Sol, colocas un termómetro y, cada diez minutos, anotas la lectura. Lo que parece un acto simple se vuelve un relato científico: una curva tiempo–°C que habla de energía solar, ganancias térmicas, pérdidas por convección y radiación, y de cómo pequeños cambios de diseño (color del fondo, pantalla reflectante, viento, tapa) cambian la historia.

Tu objetivo no es “calentar agua” sin más. Tu objetivo es entender el proceso y cuantificarlo: cuánta energía absorbió el agua, cuánta se perdió, qué tan eficiente fue tu montaje y cómo mejorarías el prototipo para el siguiente ensayo.

2) ¿Qué estamos midiendo exactamente?

Este experimento observa la transferencia de calor desde la radiación solar hacia una masa de agua contenida en una botella PET. En palabras simples: la luz golpea la botella y el líquido, parte de esa energía se convierte en calor y hace que la temperatura del agua aumente con el tiempo. Mientras eso ocurre, también hay pérdidas: el agua se enfría a la vez por contacto con el aire (convección), por la propia emisión de calor (radiación) y por conducción hacia las superficies de apoyo.

Trabajaremos con tres ideas clave, explicadas primero de forma intuitiva y luego con fórmulas.

Intuitivo: más Sol, superficies oscuras, menos viento y mejor “envolvente” significan más temperatura.
Técnico: el agua gana calor a una tasa proporcional a la irradiancia incidente y pierde a una tasa proporcional a la diferencia de temperatura con el ambiente y a los coeficientes de transferencia del montaje.

3) Diseño del montaje (y por qué cada detalle importa)

Para que el experimento sirva didácticamente y sea replicable, conviene trabajar con volúmenes modestos (por ejemplo, 500 mL). Con medio litro verás cambios apreciables en 60–90 minutos sin necesidad de condiciones extremas.

En un primer ensayo, utiliza una botella PET transparente de 1–1.5 L con 500 mL de agua. Ubícala sobre una base aislante (cartón grueso o foam) y tápala para reducir corrientes de aire sobre la boca. Colócala con un fondo oscuro detrás (cartulina negra o una lámina pintada de negro mate) y, si puedes, añade una pantalla reflectante de papel aluminio en forma de “U” abierta hacia el Sol. El aluminio devuelve fotones a la botella; el negro absorbe con más eficiencia.

La orientación es sencilla: coloca el conjunto mirando al Sol, de modo que el brillo del aluminio “bañe” la botella. En días con brisa, colócala en una zona protegida del viento; el viento aumenta las pérdidas por convección y “aplasta” la curva de calentamiento.

4) Cómo medir bien (sin convertir la clase en una receta)

Mide la temperatura del agua con un termómetro digital de sonda o un termómetro de cocina, introduciendo la punta a media altura del líquido. Anota también la temperatura ambiente, el estado del cielo (despejado, nubes finas, nublado parcial) y, si lo tienes, un dato aproximado de velocidad del viento (basta con describir “calmo”, “brisa suave”, “viento”).

Tu bitácora debe registrar hora exacta y temperatura cada 10 minutos durante al menos 60 minutos. Esa resolución es suficiente para dibujar la curva sin interrumpir el aprendizaje con mediciones obsesivas. Si hay nubes densas que tapen el Sol, anótalo: en la gráfica verás “escalones” o mesetas que cuentan lo que pasó.

5) La física detrás (en dos capas: clara y formal)

5.1 Versión clara

El aumento de temperatura se debe a que el agua absorbe parte de la radiación. La botella y el aire caliente alrededor le “cobran” energía en forma de pérdidas. Al principio, cuando el agua está fría, la diferencia con el ambiente es pequeña y el calentamiento es más rápido; conforme se acerca al ambiente (o lo supera), las pérdidas crecen y la curva se aplana. Por eso tus datos rara vez serán una línea recta: la naturaleza “negocia” entre ganancias y pérdidas.

5.2 Versión formal mínima

La energía que gana el agua en un intervalo $\Delta t$ se aproxima con:

$$Q_{\text{ganada}} \approx m \, c_p \, \Delta T$$

donde $m$ es la masa de agua (kg), $c_p$ su calor específico ($\approx 4{.}186\,\text{kJ/kg·K}$) y $\Delta T$ el cambio de temperatura (K).

La potencia solar que incide sobre un área efectiva $A$ es:

$$P_{\text{solar}} \approx G \cdot A$$

con $G$ la irradiancia (W/m²). En condiciones de Sol pleno, toma $G \approx 800–1000\ \text{W/m}^2$; con nubes ligeras, 400–700.

Las pérdidas pueden representarse de forma lumped como:

$$P_{\text{pérdidas}} \approx U \cdot A_{\text{perd}} \cdot \big(T_{\text{agua}} - T_{\text{amb}}\big)$$

donde $U$ captura el efecto combinado de convección y radiación del montaje. No necesitas calcular $U$ para aprender; basta reconocer que crece cuando hay viento, superficies frías o mucha área expuesta sin aislamiento.

6) Un ejemplo con números (para “ver” la energía)

Supón $m=0.5\ \text{kg}$ (500 mL), T_0 = 22\,^\circ\text{C} y tras 60 min mides T_1 = 40\,^\circ\text{C}.
Entonces, $\Delta T = 18\,\text{K$y:

$$Q \approx 0.5 \times 4.186 \times 18 \approx 37.7\ \text{kJ} \;\; \big(\approx 10.5\ \text{Wh}\big)$$En una hora, tu agua “guardó” ~10.5 Wh. Si el área eficaz que recibió Sol fue de 0.02 m² (aprox. la proyección de media botella) y $G=900\ \text{W/m}^2$, la energía disponible fue: $$E_{\text{incidente}} \approx G \cdot A \cdot t \approx 900 \times 0.02 \times 1\ \text{h} \approx 18\ \text{Wh}$$Una “eficiencia bruta” simple sería $10.5 / 18 \approx 58\%$. No es un valor absoluto —el área real “útil” cambia con el ángulo, la reflexión del aluminio y el sombreado—, pero te da orden de magnitud y te permite comparar ensayos (con y sin pantalla, con y sin fondo negro, con y sin viento).

7) Cómo producir tu gráfica tiempo–°C (y leerla como un científico)

Lleva tus datos a Google Sheets/Excel. Columna A: tiempo en minutos (0, 10, 20, 30…); columna B: temperatura del agua; columna C: temperatura ambiente. Inserta un gráfico de líneas y etiqueta ejes con claridad.

Al observar la curva:

• Inicio más empinado: baja diferencia de temperatura con el ambiente y menos pérdidas → calienta rápido.

• Tramo medio: si el Sol es constante, verás un incremento casi lineal por un rato.

• Tramo final: la pendiente disminuye; el sistema se acerca a un equilibrio dinámico entre ganancias y pérdidas.

• Mordidas o mesetas: nubes o ráfagas de viento; anótalas en la bitácora y cuéntalas junto a la curva.

Si anotas el estado del cielo, podrás explicar la forma de la curva. Eso, más que el número final, es lo que distingue un informe científico de un “intento de receta”.

8) Lo que más afecta tu resultado (y cómo dominarlo con diseño)

La superficie oscura (absorbedor) y la pantalla reflectante son tus mejores aliados: multiplican fotones disponibles y transforman más luz en calor. El viento es el gran enemigo silencioso; si sopla, “roba” calor con rapidez. Por eso una base aislante y una posición algo resguardada marcan diferencias notables.

La tapa importa. Destapada, el aire caliente escapa; tapada, el aire se estabiliza y ayuda a la ganancia térmica. Si el PET se deforma por calor en montajes muy optimizados, baja la radiación o aléjalo de superficies hirviendo (no es lo común con 500 mL y exposición moderada, pero anótalo).

9) Una narrativa de mejora: del primer ensayo al prototipo “2.0”

En el Ensayo 1 tu curva subió de 22 °C a 36 °C en 60 minutos. Aprendiste que el viento enfriaba la botella por un costado. En el Ensayo 2, agregaste una “U” de aluminio y una cartulina negra; ahora subiste a 40 °C. Para el Ensayo 3, moviste el montaje 15° y lo acercaste a una pared clara que rebotaba luz: alcanzaste 44 °C. Sin cambiar el Sol, cambiaste el diseño. Tus datos no son mejores “por suerte”; son mejores porque entendiste las pérdidas y actuaste sobre ellas.

Ese es el aprendizaje que buscamos: pasar del “calenté agua” al “optimizamos un sistema térmico escolar con evidencia”.

10) Seguridad y responsabilidad (porque la ciencia también cuida)

Usa botellas limpias y agua potable si habrá contacto humano. Manipula el montaje con cuidado cuando esté caliente. Evita dejar materiales brillantes cerca de ojos o superficies inflamables. No sumerjas termómetros eléctricos que no sean sumergibles. Y, por favor, no bebas el agua del experimento a menos que hayas garantizado higiene, envase apto y protocolo.

11) Qué sigue en la serie (enlace interno que retiene)

Si te gustó medir y optimizar, el siguiente escalón es aplicar ese rigor en un sistema eléctrico pequeño que almacena energía del día para usarla en la noche. Te propongo continuar con Mini panel solar para cargar celulares (FV): dimensionaremos Wh, compararemos PWM vs. MPPT en pequeño formato y diseñaremos protecciones simples para un uso seguro en aula.

12) Resumen en una línea

Calentar agua con una botella PET es sencillo; convertirlo en ciencia útil exige medir, graficar y entender cómo las ganancias solares compiten con las pérdidas, y cómo el diseño inclina la balanza.